[memo] 巡回セールスマン問題

• 概要
• ILP モデル
  • 目的関数
  • 制約条件
• 計算結果
  • $|V|=5$ の例
  • 計算時間の例

概要

典型問題． ソルバや計算機性能の確認用．

ILP モデル

目的関数

\[\begin{equation} \min \ \sum_{(u,v)\in E} c_{uv}x_{uv} \end{equation}\]

制約条件

• flow conservation

\[\begin{equation} \begin{array}{cc} \sum_{v\in V,v\ne u}x_{uv} = 1 & (u\in V) \\ \sum_{u\in V,u\ne v}x_{uv} = 1 & (v\in V) \end{array} \end{equation}\]

• Miller-Tucker-Zemlin constraints¹

\[\begin{equation} \begin{array}{cc} w_u+1-(n-1)(1-x_{uv})\le w_v & (u,v=1,2,\cdots,n-1,u\ne v) \end{array} \end{equation}\]

• variable

\[\begin{equation} \begin{array}{cc} 1\le w_v\le n-1 & (v\in V \setminus \{0\})\\ x_{uv}\in \{0,1\} & (u,v\in V)\\ w_u\in \mathbb{R} & (u\in V) \end{array} \end{equation}\]

計算結果

$|V|=5$ の例

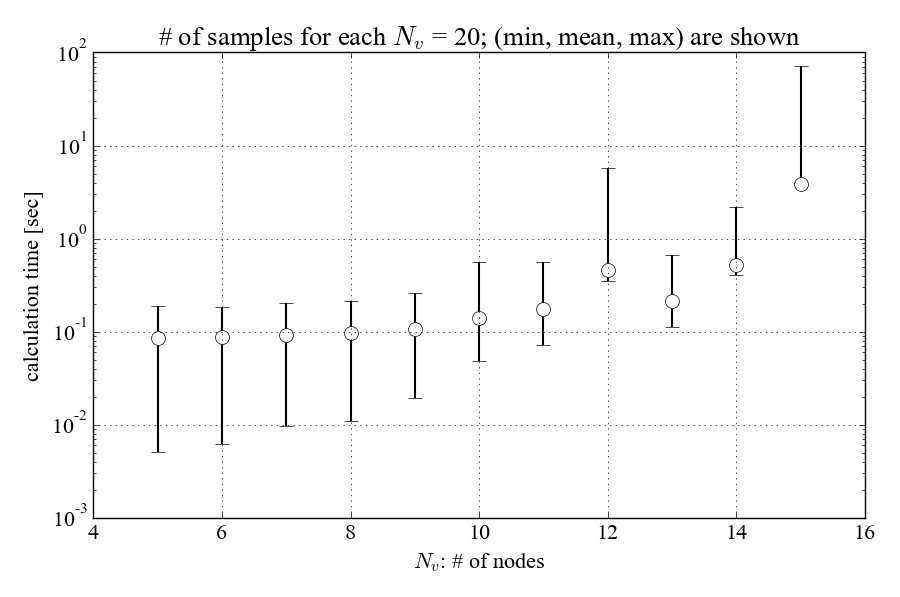
計算時間の例

import numpy as np
import pynet as pn

f = './calculation_time.csv'
# output .csv
pn.mp.ilp.tsp.evaluate_calculation_time(
    filename=f,
    nvs=np.arange(5,16),
    nsample=20
    )
# read .csv and plot
pn.mp.ilp.tsp.show_calculation_time(filename=f)

---

1. M. Desrochers and G. Laporte, “Improvements and extensions to the Miller-Tucker-Zemlin subtour elimination constraints”, Operations Research Letters 10, 27–36 (1991) ↩